
Afin d’avoir une vue commune et la possibilité de communiquer sur une métrique compréhensible de tous, il faut faire certains choix, ici, nous traiterons de celui qui a été fait en finance de marché sur la temporalité. Actuellement, la majorité des projets / productions fonctionnent en temps discret, quelques méthodologies en finance de marché prennent en compte la continuité du temps mais finissent par donner une représentativité du temps sur un horizon temporel fixe, très souvent journalier. Les départements de risque par exemple appliquent généralement des chocs en T+1, basé sur les données récoltées la veille.
__________________________
Quelle est la légitimité de représentation du temps ? Quelle est la réalité de la linéarité du temps dans notre perception du risque ? La multiplicité des scénarios à horizon temporel court tente-t-il de remplacer la conception mentale d’une modélisation théorique des phénomènes de marché compte tenu du temps ? L’état de l’art de la perception du temps est assez homogène, le temps est considéré comme une variable référentielle, linéaire et continue, une toile de fond sur lequel viennent se fixer les différentes variables. Dans quelle mesure la représentation du temps en tant que variable continue est-elle adéquate pour modéliser la complexité des phénomènes économiques et financiers ? Existe-t-il des approches alternatives pour représenter le temps en finance de marché qui pourraient mieux capturer la dynamique et l’incertitude des processus économiques ?
L’objectif de ce travail court est donc d’imaginer une possibilité théorique pertinente et utilisable en finance de marché pour mieux exprimer la dynamique d’une sensibilité en fonction du temps
__________________________
- Etat de l’art de la représentation du temps et de son utilisation courante en finance et en physique
Afin de représenter l’état de l’art de la temporalité en finance de marché, considérons que le temps est majoritairement pris en compte sur deux grands horizons :
- un horizon court terme généralement à un jour mais qui peut être élargi à une semaine
- un horizon long terme, exprimée en trimestre, semestre ou année
Sur l’horizon court terme, le temps est appréhendé comme un saut, un passage discret d’un état à un autre, un mouvement local normalement synthétique qui est souvent analysé uniquement sous le prisme de l’analyse d’un ensemble de variable. Les déformations des corrélations entre les variables ne sont pas ou peu utilisées. Cet horizon est très simple à analyser, compréhensible par tous, mais fatalement manque de précision sur la déformation des sensibilités par rapport au temps autres que celles synthétisées par les sensibilités (ou grecques) de deuxième ou troisième degré (ex : Charm ou Veta) qui elles aussi sont peu utilisées.
Sur l’horizon long terme, le temps est une référence de classement, Q1, S2, la temporalité est considérée comme un marque page sans corrélation avec l’écoulement du temps, chaque période est un instantané ponctuel, séparé des autres, sans communication temporelle. Le temps est une référentiel mort, n’impactant pas de dynamique puisque dynamique il n’y a pas. Cette absence de dynamique provient principalement de l’absence de définition de certains concepts standards tels que la masse comme je le présenterai plus tard.
Quelques études tentent toutefois de considérer la temporalité comme une variable intrinsèque comme les travaux de Mandelbrot, développés dans les années 90 par Edgar E. Peters[1] puis perfectionnés par Cao, He & Cao[2]. Ce dernier ouvrage apportant un potentiel trait d’union entre la physique théorique contemporaine et la finance de marché
L’état de l’art en physique perçoit le temps très différemment, si nous reprenons la notion physique d’espace-temps, tout corps va à la vitesse de la lumière, un objet immobile dans l’espace va à la vitesse de la lumière dans le temps. Aussi, plus vite un corps se déplace vite dans l’espace, plus lentement il va dans le temps. (cf paradoxe des jumeaux de Langevin[3]). Bien-sûr appliquer des théories aussi avancées serait très complexes à mettre en place mais cet état de l’art avait pour unique but de mettre en avant la place primordiale que le temps possède dans la compréhension des phénomènes physiques. Cependant, si nous nous interrogeons sur ce qui peut exister dans d’autres sciences concernant la visualisation d’un flux (en finance une sensibilité) dépendant du temps, il existe d’autres concepts plus facilement conciliables.
L’idée de ce travail n’est pas de déterminer une conjecture générale permettant d’expliciter tous les prismes analytique en posant un référentiel temporel intégré, nous nous contenterons de considérer que les sensibilités sont dynamiques et donc sont en mouvement avec le temps et que nous avons besoin de pouvoir définir la position d’un point en un temps donné.
Aussi, présentons deux axiomatiques qui sont la cinématique Lagrangienne et la cinématique Eulérienne en dérivée particulaire. Ces deux cinématiques sont utilisées pour la première dans la définition des trajectoires en mécanique classique et générale pour les solides indéformables[4] et la seconde pour l’analyse des champs vectoriels, de champs eulérien de vitesse, principalement en mécanique des fluides. [5]
Ici l’objectif sera d’apporter une vue sur des principes physiques connus et simples et de projeter leur utilisation potentielle sur un exemple en fil rouge tout au long de la présentation, une matrice de vol de taux.
__________________________
- Description de la mécanique générale au travers de la cinématique Lagrangienne
Concernant la cinématique Lagrangienne, on cherche à suivre la variation ou le mouvement d’un point situé dans un espace au cours du temps.
Tout d’abord représentons en des termes simples les dits principes de mécanique générale
Ici nous analysons la position à tout instant « t » d’une particule et nous pouvons donc évaluer sa trajectoire par sa vitesse :
[1] Fractal Market Analysis: Applying Chaos Theory To Investment And Economics, Edgar E. Peters
[2] Multifractal Detrended Analysis Method and Its Application in Financial Markets, Guangxi Cao (Author), Ling-Yun He (Author), Jie Cao (Author)
[3] https://gallica.bnf.fr/ark:/12148/bpt6k111220/f39
[4] Mécanique générale, J.-C. Bône, J. Morel et M. Boucher
[5] Mécanique des fluides, D. Desjardins, M. Combarnous, N. Bonneton
Concernant la cinématique Lagrangienne, on cherche à suivre la variation ou le mouvement d’un point situé dans un espace au cours du temps.
Tout d’abord représentons en des termes simples les dits principes de mécanique générale
Ici nous analysons la position à tout instant « t » d’une particule et nous pouvons donc évaluer sa trajectoire par sa vitesse :
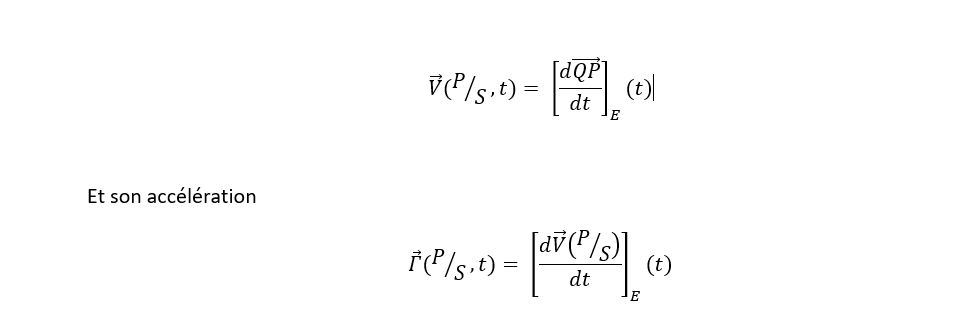
Dans la cinématique Lagrangienne, la vitesse et l’accélération jouent un rôle fondamental pour comprendre le mouvement des particules. La vitesse d’une particule représente la variation de sa position par rapport au temps, tandis que l’accélération mesure la variation de sa vitesse.
En d’autres termes, la vitesse nous indique à quelle vitesse la particule se déplace et dans quelle direction, tandis que l’accélération nous renseigne sur la rapidité avec laquelle cette vitesse change. Ces concepts sont essentiels pour analyser les trajectoires des particules et comprendre les forces qui influent sur leur mouvement. Par exemple, dans un mouvement rectiligne uniformément accéléré, la vitesse augmente régulièrement au fil du temps, ce qui se traduit par une accélération constante.
Au niveau terminologique, ajoutons que « S » représente un référentiel auquel ou va analyser la vitesse d’un point « P » et « ε » est un espace affine euclidien de dimension 3. Ainsi est appelé un « système de référence » ou espace-temps ou référentiel observateur avec « T » qui est un espace affine de dimension 1 dont les points sont appelés « instants »
Ces éléments basiques vont être inclus dans un premier temps dans la définition de la vitesse lagrangienne, la vitesse cinématique de Lagrange

Que nous pouvons interpréter par la phrase : « pour une variation d’un bp de taux d’intérêt, l’accélération de l’action est de 0.5 euro par heure » qui exprime donc l’influence de la dynamique de l’action sur le marché au travers des variables prises en compte.
Cette représentation peut être appliquée sur une matrice avec un mouvement aléatoire qui sera commun à tous les exemples d’application par la suite. Ici avec déformation de la nappe
La variable 1 est par exemple les ténors et la variable 2 la maturité (ici les données sont en positifs négatifs mais évidemment dans un cadre d’application strict on reprendrait les plots standards en finance de marché). L’axe Z sera identifié comme « masse » par défaut, car nous commençons par un exemple de déformation d’un plan mais n’est pas à prendre comme une « masse » au sens physique.
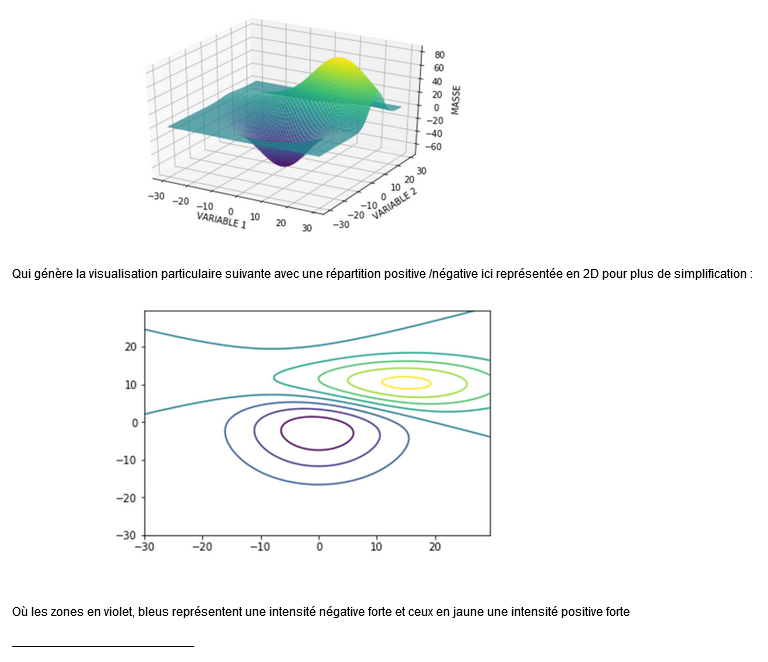
- Présentation de la mécanique des fluides avec la notion de cinématique Eulérienne
Concernant la cinématique Eulérienne, on ne cherche pas à définir un point précis car ce n’est pas possible en mécanique des fluides, on étudie donc le mouvement d’un flux par unité de temps.
Ici le champ Eulérien des vitesses vu par le prisme de la mécanique des fluides


Que nous pouvons écrire « = 0 » si pour prouver la conservation de la masse, cependant, cela nécessiterait de résoudre les intégrales, nous pourrions nous mettre dans un cas de figure ou le domaine est perçu comme un écoulement sur un sol sinusoïdal où les paramètres de superpositions des écoulements ou la rugosité pourraient être simplifié. En définissant la longueur d’onde généralement nommée « λ », nous pourrions vérifier la convergence de la formule en « = 0 » validant la conservation de la masse au travers une grille discrétisée pour évaluer la masse et la divergence sur chaque point de la grille afin de valider l’hypothèse de conservation.
- Introduction de l’électromagnétisme et réconciliation de la mécanique générale et de la mécanique des fluides
Ainsi l’idée est de concilier cinématique Lagrangienne et Eulérienne pour permettre d’exprimer l’accélération qui est un concept Lagrangien, cela se fait assez naturellement par l’introduction de l’électromagnétisme[1] et plus précisément par les lois de conservation de la charge qui reprend les principes de la cinématique et de la cinétique exprimé auparavant s’ajoutant à la conservation de la masse.
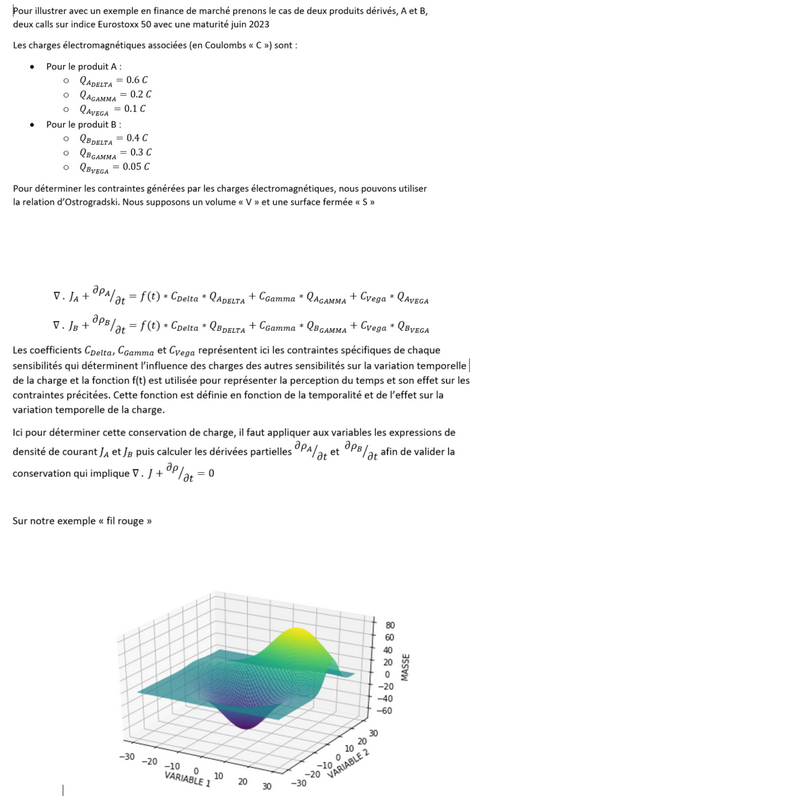
Afin d’introduire au plus grand nombre l’électromagnétisme, posons la grandeur « G » indispensable pour comprendre les développements suivants :
[1] Electromagnétisme : Milieux, structures, énergie. Jean-Marcel Rax

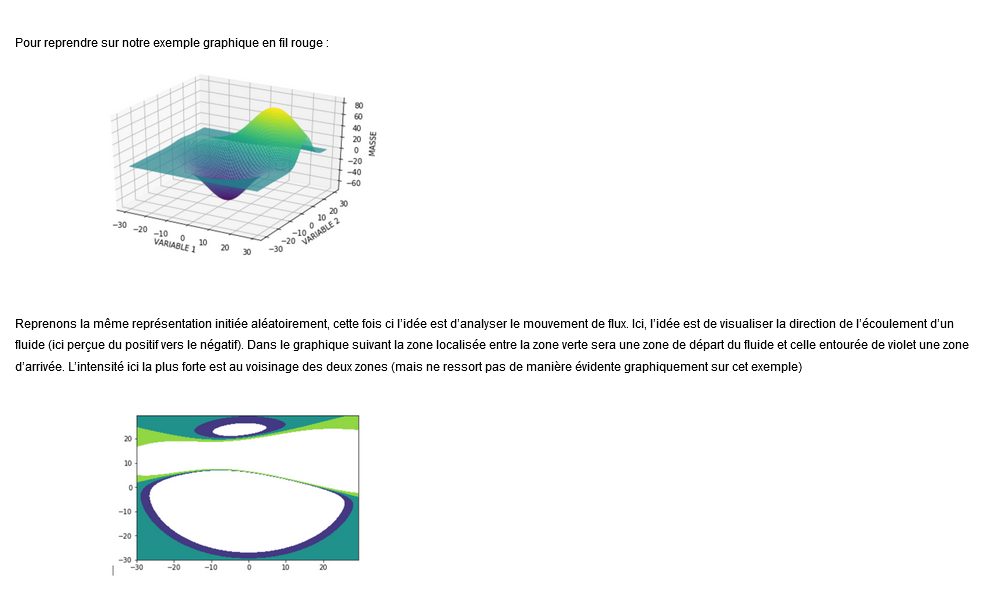
Reprenons la même représentation initiée aléatoirement, cette fois ci l’idée est d’analyser le mouvement de flux. Ici, l’idée est de visualiser la direction de l’écoulement d’un fluide (ici perçue du positif vers le négatif). Dans le graphique suivant la zone localisée entre la zone verte sera une zone de départ du fluide et celle entourée de violet une zone d’arrivée. L’intensité ici la plus forte est au voisinage des deux zones (mais ne ressort pas de manière évidente graphiquement sur cet exemple)
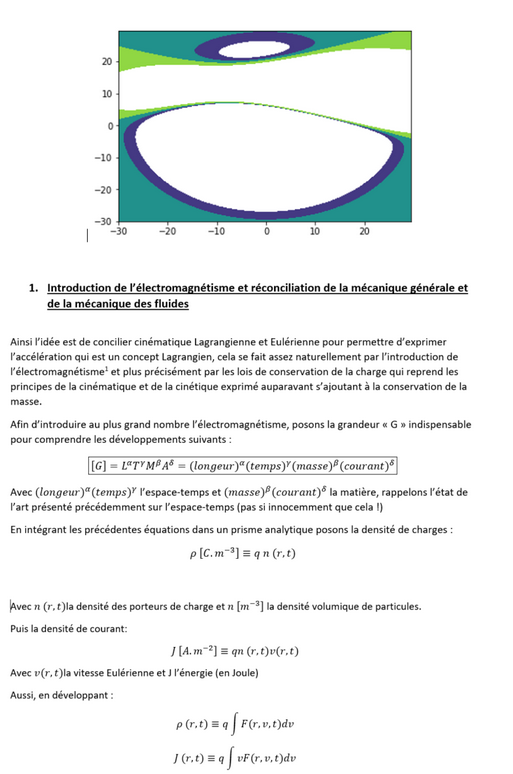

Cette fois-ci prenons l’écoulement du temps générant un mouvement vers le haut de la variable 2, ce qui modifie le référentiel du plan de base, on dénote également sur la variable 2 au point 0 l’apparition d’une discontinuité involontaire.
Cette représentation propose l’idée que l’écoulement même du temps génère un mouvement spontanée, en effet, les matrices de volatilité sont généralement représentées ayant pour colonne leur maturité, la maturité s’écoulant au passage du temps. Ainsi, l’écoulement du temps du temps représenterai la génération première de dynamique de mouvement et initierai les premières interactions (serait semblable à une rupture spontanée en quantique)
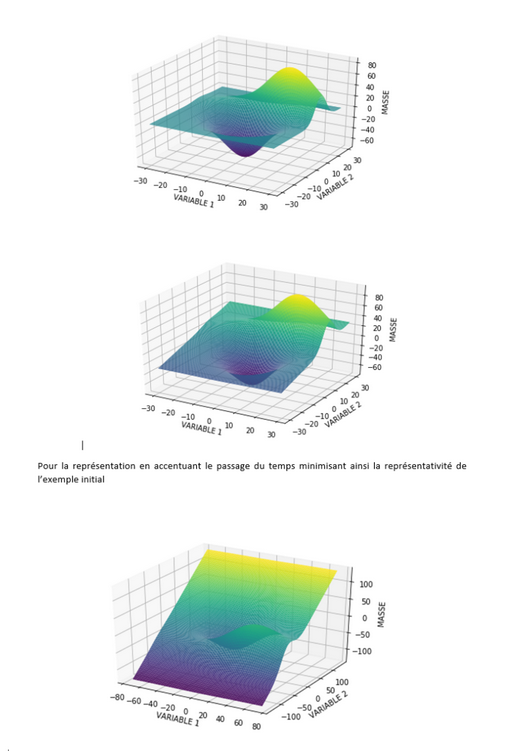
Où cette fois-ci l’état de l’art initial est complètement noyé par le passage du temps qui domine tout. Ici la charge est donc majoritairement temporelle et finalement l’interaction des deux parties positives et négatives n’apparait que très peu ce qui est contraire à ce qui aurait dû apparaître et nécessiterai plus de modélisation

- Conclusion et ouverture
La présence ici construite de la temporalité dans un mouvement particulaire est évidemment incomplet pour spéculer sur une potentielle utilisation du temps et par corolaire de la conservation des charges en finance de marché et nécessiterai un travail bien plus conséquent. Cependant, cet article a pour ambition d’envisager une approche différente de la perception du temps, de la dynamique des mouvements et de la représentativité des sensibilités vus comme un mouvement couplé de particule et de fluide et possédant une masse et une énergie. On pourrait imaginer, si la représentation est développée et qu’elle est mathématiquement possible (certainement), qu’une matrice de sensibilité deviendrait un volume intégrant les variables précédemment cités, un ensemble continu, ayant une dynamique d’ensemble mais aussi des interactions de variables internes.
Ici nous n’avons pas étudié la notion de tenseur, de torseur ou de polarisation qui sont les trois notions pouvant à mon sens apporter un apport matériel sur la capacité d’ingestion de la notion de sensibilité par des lois physiques liant mécanique générale, mécanique des fluides et électromagnétisme.
Encore une fois l’objectif est de proposer une méthodologie différente, d’explorer d’autres méthodologies, connues en physique et d’analyser leur pertinence et leur efficience en économie et plus précisément sur les marchés financiers.
En plus de l’ajout de notion telle que la masse et l’énergie ainsi que l’impact de la temporalité déroulé durant cet article, l’ajout également d’un système d’unité différencié, qui ne serait pas forcement exprimé en €, sera probablement nécessaire.
Loïc Kolodziejczak
Consultant Pôle Risques et Modélisation



