
Depuis janvier 2020, LCL et CMG Conseil se sont associés autour d’un partenariat académique en s’appuyant sur notre thésard CIFRE. Il repose sur l’utilisation de nouvelles techniques mathématiques afin de mieux appréhender les futures modélisations en risque de crédit. Du développement de nouveaux algorithmes à l’utilisation du machine learning, notre partenariat devrait permettre d’éprouver de nouvelles techniques de modélisation sur les données du LCL grâce à l’appui de la recherche opérationnelle mise en place chez CMG Conseil.
Faire de vos données une expérience inédite !
Notre approche offre de nombreuses perspectives d’évolution dans la modélisation du risque :
- Segmentation : Mieux appréhender les liens forts entre le risque et toutes les données disponibles, ce sera un gage d’efficacité future.
- Modélisation : Mieux expliquer les liens des données historisées, ce sera une voie vers l’utilisation de nouvelles méthodes de modélisation.
- Performance : Mieux comprendre les données historisées, ce sera l’apport d’une meilleure efficacité des modèles prédictifs.
Parmi ces perspectives, nous présentons en détails quelques outils mathématiques et algorithmiques qui pourront aider à la segmentation. En particulier, nous nous intéressons à la problématique de la segmentation des variables : comment sélectionner les variables les plus pertinentes pour comprendre/prédire le défaut de crédit ?
De nombreux outils statistiques et de machine learning sont disponibles pour répondre à cette question. En commençant par les méthodes les plus connues, nous proposons d’explorer différentes approches en s’intéressant à leurs caractéristiques.
Les outils principaux
Analyse par composante principale
Une première analyse de composante principale (ACP) pourrait nous guider sur les variables les plus explicatives. En effet, une ACP permet d’une part de visualiser l’ensemble des clients, d’autre part de mesurer l’apport de variance des variables. Essentiellement, on transforme (ou on projette) les données tout en préservant la variance au sein de nos données.

Explication de variance en fonction des axes d’une ACP
Bien que cette méthode s’avère efficace pour un premier contact des données, elle n’est pas toujours adéquate pour répondre à notre problématique de segmentation de variables. La qualité de la projection n’est pas toujours garantie puisqu’elle se base sur des liens linéaires entre les variables. Aussi, l’explication de la variance ne signifie pas nécessairement le pouvoir prédictif pour variable cible (ici variable défaut).
Importance des variables.
La sélection de variables peut être vue aussi comme un problème de classement des variables. L’idée étant d’attribuer une mesure de pouvoir explicatif de chaque variable. Les arbres de décisions sont un de bons candidat puisqu’ils permettent de mesurer le pouvoir discriminant de chaque variable.
Pour ce faire, on commence par modéliser le défaut avec l’ensemble des variables à l’aide des arbres de décision. Lorsque le modèle est entraîné, on peut identifier et mesurer les variables qui ont le plus contribué à la construction des arbres. Il suffira alors de trier les variables en fonction de cette mesure pour sélectionner les plus pertinentes. La mesure utilisée est alors appelée importance des variables.
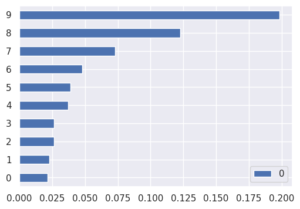
Importance de variables à l’aide d’un Boosting d’arbres
En revanche, cette sélection de variables sera dépendante des modèles d’apprentissage. Par conséquent, la tâche principale revient à une modélisation robuste de la variable cible. Il faudra alors étudier tous les aspects d’une modélisation machine learning (hyper paramètres tuning, performance, etc.) pour s’assurer de la stabilité de la sélection de variables.
Mesurer l’information
Sélectionner en fonction de l’information
En fin de compte, ce que nous cherchons dans les données, ce sont les informations relatives au défaut : Quelles sont les informations les plus pertinentes au sein de mais données ? Comment les quantifier ? Une réponse peut se trouver à l’aide de la théorie d’information. L’information mutuelle est une mesure qui permet de quantifier la dépendance entre deux variables. Intuitivement, elle mesure la part d’incertitude qu’on pourrait réduire lorsqu’on connaît la seconde variable.
Dans la même philosophie que l’importance des variables, on se sert de cette mesure pour identifier les variables les plus pertinentes pour la variable défaut :
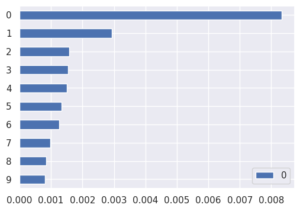
Sélection de variables avec l’information mutuelle
Algorithme de recherche glouton
Cette approche comprend deux notions qui nous amènent à une sélection de variable plus fine : la pertinence et la redondance. La pertinence mesure l’apport d’une variable pour expliquer le défaut. Quant à la redondance, elle pénalise lorsque deux variables apportent les mêmes informations relatives au défaut, auquel cas une seule des deux variables suffirait. Ainsi les algorithmes de sélection de variables basés sur l’information mutuelle ressortiront les variables pertinentes et inédites.
Visualiser les liens des variables
Si on a pu visualiser l’ensemble des individus à l’aide d’une ACP, il peut être intéressant de représenter les variables en identifiant les liens entre elles. Cette fois-ci, l’information mutuelle sera utilisée pour mesurer la similarité entre les variables. L’idée est de rapprocher les variables en groupe qui partagent les mêmes informations.
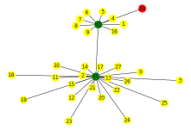
Visualisation des liens des variables
La variable défaut en rouge
A l’aide de cette visualisation, on pourra sélectionner les variables pertinentes au défaut en repérant le groupe de variable le plus proche. Ce sont en effet les variables qui partagent le plus d’information avec le défaut.
Plus généralement, cette approche permet d’apercevoir la structure des données en grande dimension pour analyser les liens entre les variables.
La sélection de variables reste un défi pour les modélisateurs puisqu’il n’y a pas une unique manière de procéder. On propose ici quelques approches classiques mais aussi moins habituels qui pourront ressortir les variables les plus pertinentes pour modéliser le défaut. En présence de plusieurs méthodes de sélection, on pourra comparer et analyser les résultats des sélections pour renforcer ou approfondir la modélisation.
SH.Pang & B.Etienne


